2.3 Clasificación de las Matrices.

Triangular superior: 

En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.

Triangular inferior:

En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros.

Diagonal:

En una matriz diagonal todos los elementos situados por encima y por debajo de la diagonal principal son nulos.

Escalar:

Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.

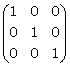
Identidad:

Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.

Potencia:

Se llama potencia k-ésima de una matriz cuadrada A, donde k OE Õ, un entero positivo, al producto de A por sí misma, repetido k veces.

Ak =A⋅A⋅A⋅......k veces ...... ⋅A

Se conviene en que:

A- k = (A- 1) k " k OE Õ

A0 = I

Traspuesta:

Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas

(At)t = A

(A + B)t = At + Bt

(α ·A)t = α· At

(A · B)t = Bt · At

Simétrica:

Una matriz simétrica es una matriz cuadrada que verifica: A = At.

Antisimetrica:

Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica: A = -At.

Compleja:

Sus elementos son números complejos aij e ¬

Conjugada:

Matriz conjugada de una matriz A Aquella que se obtiene sustituyendo cada elemento por su complejo conjugado (igual parte real, pero la parte imaginaria cambiada de signo).

Hermitiana o hermitica:

Una matriz hermitiana (o hermítica) es una matriz cuadrada de elementos complejos que tiene la característica de ser igual a su propia traspuesta conjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para todos los índices i y j:

o, escrita con la traspuesta conjugada A*: Por ejemplo,

es una matriz hermítica.

Antihermitiana:

una Matriz antihermitiana es una matriz cuadrada cuya traspuesta conjugada es menos la matriz. Esto es si satisface a la relación:

A * = -A

o en su forma componente, si (A = ai,j):

Para todas las i y las j.

Ortogonal:

Una matriz ortogonal es necesariamente cuadrada e invertible : A-1 = AT La inversa de una matriz ortogonal es una matriz ortogonal. El producto de dos matrices ortogonales es una matriz ortogonal. El determinante de una matriz ortogonal vale +1 ó -1.

FUENTE: http://itsavbasicas.blogspot.mx/2012/05/23-clasificacion-de-las-matrices.html